Physics-inspired graph neural networks to solve combinatorial optimization problems
Combinatorial optimization problems are complex problems with a discrete but large set of possible solutions. Some of the most renowned examples of these problems are the traveling salesman, the bin-packing, and the job-shop scheduling problems.
Researchers at the Amazon Quantum Solutions Lab, part of the AWS Intelligent and Advanced Computer Technologies Labs, have recently developed a new tool to tackle combinatorial optimization problems, based on graph neural networks (GNNs). The approach developed by Schuetz, Brubaker and Katzgraber, published in Nature Machine Intelligence, could be used to optimize a variety of real-world problems.
“Our work was very much inspired by customer needs,” Martin Schuetz, one of the researchers who carried out the study, told TechXplore. “In our daily work at the Amazon Quantum Solutions Lab, we interact with many customers across various verticals on their journey to get quantum-ready, i.e., prepare for a future when this emerging technology will be commercially viable. Most customer use cases involve combinatorial optimization problems.”
In the context of consumer services, combinatorial optimization problems can have many different forms. Two notable examples of these problems are portfolio optimization problems in finance and job-shop scheduling tasks in manufacturing. The term portfolio optimization refers to the process through which one selects the best portfolio or asset distribution for a specific situation among a set of available portfolios.
Job-shop scheduling problems, on the other hand, occur in instances where a set of jobs or tasks must be performed and there is a limited set of resources/tools to perform these tasks. In these cases, one could be asked to find an optimal schedule that utilizes available tools to perform the tasks in as little time as possible.
As quantum technology is still in its early stages of development, researchers have been trying to develop optimization tools that do not fully rely on quantum computers, at least until these computers have become commercially viable. In their paper, Schuetz and his colleagues thus introduced an optimization technique based on GNNs inspired by physics.
“Given their inherent scalability, physics-inspired GNNs can be used today to approximately solve (large-scale) combinatorial optimization problems with quantum-native models, while helping our customers get quantum-ready by using the mathematical representation that quantum devices understand,” Brubaker said.
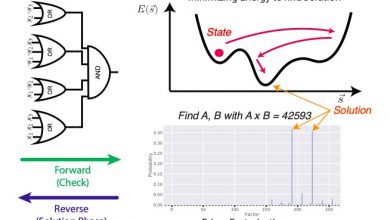
The approach developed by Schuetz and his colleagues first identifies the Hamiltonian (i.e., cost function) that encodes the specific optimization problems that one is trying to solve. Subsequently, it associates the corresponding decision variables with nodes within a graph.
“Our key idea is then to frame combinatorial optimization problems as unsupervised node classification tasks whereby the GNN learns color (in other words, spin or variable) assignments for every node,” Schuetz explained. “To this end, the GNN is iteratively trained via a custom loss function that encodes the specific optimization problem of interest, in a one-to-one correspondence with the original Hamiltonian, thus providing a principled choice for the GNN’s loss function.”
After the GNN was trained, the team projected the final values for the soft node assignments it produced to hard class assignments. This ultimately allowed them to approximately solve large-scale combinatorial optimization problems of interest.
The approach proposed by Schuetz and his colleagues has several advantages over other methods to tackle combinatorial optimization problems. Most notably, their method is highly scalable, which means that it could be used to computationally optimize complex problems with hundreds of millions of nodes.
“Our GNN optimizer is based on a direct and general mathematical relation between prototypical Ising spin Hamiltonians and the differentiable loss function with which we train the GNN, thereby providing one unifying framework for a broad class of combinatorial optimization problems and opening up the powerful toolbox of physics to modern deep-learning approaches,” Brubaker said. “Fusing concepts from physics with modern machine learning tooling, we propose a simple, generic and robust solver that does not rely on handcrafted loss functions.”
Remarkably, the approach devised by Schuetz and his colleagues can approximately solve optimization problems without the need for training labels, which are a key requirement for all supervised learning methods. As the technique casts optimization problems as Ising Hamiltonians, it can also run natively on quantum hardware.
“We provide a unifying, interdisciplinary framework for optimization problems that incorporates insights from physics and tools from modern deep learning,” Schuetz explained. “With this framework we have a tool at our disposal that is broadly applicable to canonical NP-hard problems; prominent examples include maximum cut, minimum vertex cover, maximum independent set problems, as well as Ising spin glasses.”
In the future, the new GNN-based method introduced by this team of researchers could be used to tackle a variety of complex, real-world optimization problems. As it is inherently scalable, the Amazon Quantum Solutions Lab and AWS plan to offer it to their customers as a tool that could facilitate their transition towards quantum technologies. In fact, their technique could allow customers to approach both problems related to specific use cases in a quantum-native modeling framework, both on a small and industry-relevant scales.
“In the future, we will continue to research conceptual, theoretical, as well as more applied research questions. On the one hand we have several ideas how to improve and extend the capabilities of the proposed GNN optimizer, and on the other hand there are many applied use cases we can try to solve with this new tool. We will continue to use customer feedback to help us guide and prioritize our research agenda,” Katzgraber said.
Conclusion: So above is the Physics-inspired graph neural networks to solve combinatorial optimization problems article. Hopefully with this article you can help you in life, always follow and read our good articles on the website: Ngoinhanho101.com